A new cosmology theory suggests that our Universe has a mirror image, an “antiuniverse” that existed before the big bang.
In our Universe there’s more matter than antimatter, and time runs forward as space expands.
This seems to violate a fundamental symmetry, called CPT symmetry, that says physics is unchanged when time, space, and matter-antimatter are all flipped. To balance out the cosmos, Latham Boyle, Kieran Finn, and Neil Turok from the Perimeter Institute for Theoretical Physics in Canada propose that the big bang was also the starting point of an antiuniverse, where time runs in the opposite direction and antimatter dominates. They show that such a CPT-symmetric model is not only consistent with the known cosmic expansion history but also provides a straightforward explanation for dark matter.
Scientists in Canada revealed a new cosmological model with the existence of an “antiuniverse” paired to our own, preserving the fundamental rule of physics called CPT symmetry.
Above, in a CPT-symmetric universe, time would run backwards from the Big Bang and antimatter would dominate. Credit L Boyle/Perimeter Institute of Theoretical Physics
The team has yet to show whether this model can reproduce certain observations that the inflation scenario explains—such as the uniformity of the cosmos on large scales. However, the new model gives a natural explanation for dark matter: a CPT-symmetric Universe would produce large numbers of very massive sterile neutrinos. Such superheavy neutrinos might also be the source of recently observed high-energy cosmic-ray showers.
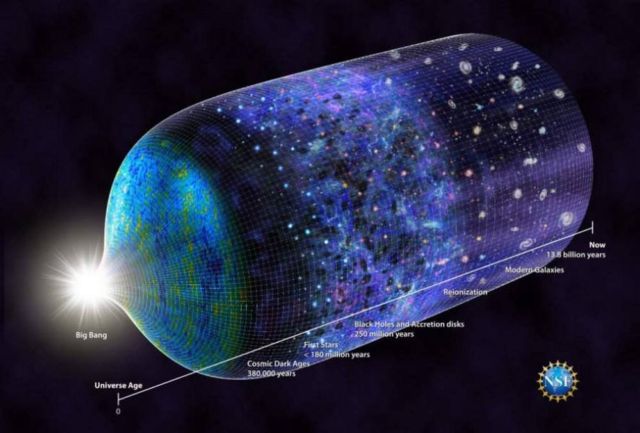
A timeline of the universe, updated to show when the first stars emerged. Credit: N.R.Fuller, National Science Foundation
via Futurism




Leave A Comment